The Multi-Armed Bandit Problem -Thompson Sampling (Ad Campaign)

# Importing the dataset

 dataset = read.csv('Ads_CTR_Optimisation.csv')

 # Implementing Thompson Sampling

 N = 10000
d = 10
ads_selected = integer(0)
numbers_of_rewards_1 = integer(d)
numbers_of_rewards_0 = integer(d)
total_reward = 0
for (n in 1:N) {
  ad = 0
  max_random = 0
  for (i in 1:d) {
    random_beta = rbeta(n = 1,
                        shape1 = numbers_of_rewards_1[i] + 1,
                        shape2 = numbers_of_rewards_0[i] + 1)
    if (random_beta > max_random) {
      max_random = random_beta
      ad = i
    }
  }
  ads_selected = append(ads_selected, ad)
  reward = dataset[n, ad]
  if (reward == 1) {
    numbers_of_rewards_1[ad] = numbers_of_rewards_1[ad] + 1
  } else {
    numbers_of_rewards_0[ad] = numbers_of_rewards_0[ad] + 1
  }
  total_reward = total_reward + reward
}
# Visualising the results

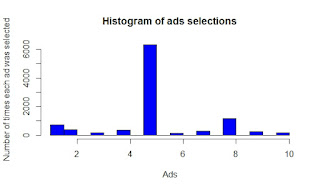
 hist(ads_selected,
     col = 'blue',
     main = 'Histogram of ads selections',
     xlab = 'Ads',
     ylab = 'Number of times each ad was selected')


Comments

Post a Comment

Popular posts from this blog

Apriori

Image
# Data Preprocessing # install.packages('arules') library(arules) dataset = read.csv('Market_Basket_Optimisation.csv', header = FALSE) #sparce matrix dataset = read.transactions('Market_Basket_Optimisation.csv', sep = ',', rm.duplicates = TRUE) distribution of transactions with duplicates: 1  5  summary(dataset) transactions as itemMatrix in sparse format with  7501 rows (elements/itemsets/transactions) and  119 columns (items) and a density of 0.03288973  most frequent items: mineral water          eggs     spaghetti  french fries     chocolate       (Other)           1788          1348          1306          1282          1229         22405  element (itemset/transaction) length distribution: sizes    1    2    3    4    5    6    7    8    9   10   11   12   13   14   15   16   18   19   20  1754 1358 1044  816  667  493  391  324  259  139  102   67   40   22   17    4    1    2    1 
Read more

Decision Tree Classification

Image
# Importing the dataset dataset = read.csv('Social_Network_Ads.csv') dataset = dataset[3:5] # Encoding the target feature as factor dataset$Purchased = factor(dataset$Purchased, levels = c(0, 1)) # Splitting the dataset into the Training set and Test set # install.packages('caTools') library(caTools) set.seed(123) split = sample.split(dataset$Purchased, SplitRatio = 0.75) training_set = subset(dataset, split == TRUE) test_set = subset(dataset, split == FALSE) # Feature Scaling training_set[-3] = scale(training_set[-3]) test_set[-3] = scale(test_set[-3]) # Fitting Decision Tree Classification to the Training set # install.packages('rpart') library(rpart) classifier = rpart(formula = Purchased ~ .,                    data = training_set) # Predicting the Test set results y_pred = predict(classifier, newdata = test_set[-3], type = 'class') # Making the Confusion Matrix cm = table(test
Read more