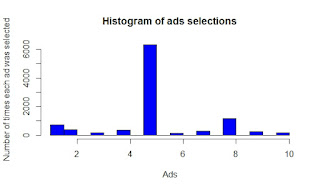
The Multi-Armed Bandit Problem -Thompson Sampling (Ad Campaign)

# Importing the dataset dataset = read.csv('Ads_CTR_Optimisation.csv') # Implementing Thompson Sampling N = 10000 d = 10 ads_selected = integer(0) numbers_of_rewards_1 = integer(d) numbers_of_rewards_0 = integer(d) total_reward = 0 for (n in 1:N) { ad = 0 max_random = 0 for (i in 1:d) { random_beta = rbeta(n = 1, shape1 = numbers_of_rewards_1[i] + 1, shape2 = numbers_of_rewards_0[i] + 1) if (random_beta > max_random) { max_random = random_beta ad = i } } ads_selected = append(ads_selected, ad) reward = dataset[n, ad] if (reward == 1) { numbers_of_rewards_1[ad] = numbers_of_rewards_1[ad] + 1 } else { numbers_of_rewards_0[ad] ...